CHAOS (physique)

CHAOS (physique)

Dans le langage usuel, le mot chaos est profondément relié à la notion de désordre total – ce que la Bible nomme le Chaos originel. Le substantif chaos peut qualifier aussi bien un agencement spatial, comme un chaos de rochers, qu’une situation collective (sociale, économique, politique, etc.) ou individuelle. Dans le domaine des sciences physiques, l’expression de chaos s’est ainsi appliquée à tout phénomène ne semblant obéir à aucune loi et étant donc, de ce fait, impossible à prévoir. Longtemps, les adjectifs «chaotique» et «aléatoire» sont restés synonymes. Nous allons voir qu’aujourd’hui le terme de chaos se rapporte à une classe de phénomènes bien définis où l’imprédictibilité est certes présente, mais où n’en existe pas moins un ordre sous-jacent.

1. Origine des phénomènes aléatoires

L’évolution temporelle d’un phénomène, une succession d’événements sont dites erratiques ou aléatoires si elles n’obéissent apparemment à aucune loi, à aucune régularité qui permettent de les prévoir. Dans ce sens, «aléatoire» est synonyme d’«imprédictible». À titre d’exemple, la variation de la pression atmosphérique en un lieu donné est erratique et, de fait, imprédictible, tant il est vrai que la connaissance de son évolution passée n’en permet pas la prévision. Au contraire, la variation de la hauteur d’eau dans un port soumis à l’influence des marées est régulière et rigoureusement prévisible.

Il existe une origine naturelle à une évolution ou à une suite d’événements erratiques: c’est l’effet d’une loi des grands nombres. Le caractère désordonné est alors lié à la conjonction d’une multitude d’événements indépendants entre eux. Prenons le cas d’une suite de nombres tirés au hasard, comme celle qui est donnée par tirage du loto. Ces suites sont par définition imprédictibles, ce qui donne précisément tout leur sel aux jeux de hasard. La cause en réside bien évidemment dans la multitude des chocs que les boules, porteuses des numéros, subissent entre elles ou de la part des bras d’agitation.

De même, dans le domaine de la physique, le mouvement brownien d’une particule, mouvement aléatoire par excellence, est lié aux multitudes de chocs que subit cette particule de la part des molécules du fluide dans lequel elle se trouve en suspension. C’est ainsi que beaucoup de phénomènes erratiques sont liés à une loi des grands nombres, telle, par exemple, la turbulence développée, qu’illustre bien la complexité de la trajectoire d’une feuille morte ballottée dans le plus grand désordre par jour de grand vent. L’origine de ce désordre est due à la coexistence d’un grand nombre de tourbillons, de toutes tailles et de toutes vitesses, qui agitent la feuille dans tous les sens.

Se pose alors une interrogation fondamentale: un comportement erratique ne peut-il avoir son origine que dans une loi des grands nombres? La réponse est non. Un exemple nous est fourni par la suite itérée:

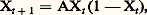où la variable X, comprise entre 0 et 1, est définie à l’instant t + 1 en fonction de ce qu’elle était à l’instant t . Partant d’une valeur initiale X⁰ (0 麗 X⁰ 麗 1), on obtient une suite de nombres X¹, X², ... Le point crucial est que, pour toute une gamme de valeurs de A (en particulier A = 4), la suite engendrée est erratique (fig. 1). Malgré le caractère très simple et parfaitement déterministe de la loi qui engendre les nombres successifs, ceux-ci sont (à temps long) aussi imprédictibles que s’ils étaient tirés à la loterie. Cela montre qu’un phénomène erratique n’est pas nécessairement lié à une loi des grands nombres, c’est-à-dire à une complexité inhérente au système. C’est ainsi que nous devons aux mathématiques l’illustration de ce fait que, contrairement à toute attente, déterminisme et chaos ne sont nullement antinomiques.

2. La sensibilité aux conditions initiales

Regardons de plus près l’aspect graphique de l’itération citée plus haut. En considérant la parabole X^t+1 = AX^t (1 漣 X^t ) dans l’intervalle [0, 1], l’itération se pratique aisément à partir d’une valeur X⁰ en se servant de la première bissectrice (fig. 1). En partant d’un point très voisin X ⁰ = X⁰ + 嗀 X et itérant de la même manière, les écarts 嗀 = X^t+1 漣 X^t+1 obtenus à chaque itération sont en moyenne supérieurs aux 嗀 X^t calculés précédemment: ils sont multipliés à chaque fois par la pente P de la parabole qui se révèle, en moyenne, être supérieure à l’unité. Un écart, une erreur initiale multipliée à chaque itération par P, croît donc, en moyenne, exponentiellement avec leur nombre. C’est dire que les deux points voisins X⁰ et X ⁰ = X⁰ + 嗀 X auront rapidement des images très différentes. Autrement dit, les deux suites:

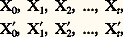un court moment semblables, différeront rapidement au point de n’avoir plus aucune ressemblance l’une avec l’autre. Ressemblantes dans le «passé», elles divergent dans le futur, d’où leur imprédictibilité. Il est nécessaire de rappeler à ce propos que la prédictibilité est fondée sur la permanence d’une ressemblance qui permet d’extrapoler, à partir de la connaissance du passé, le comportement à venir: il faudrait ici connaître le passé avec une précision infinie pour prévoir l’avenir, chose impossible en pratique. D’après ce que nous avons admis ci-dessus, la suite des itérés est donc chaotique bien que déterministe du fait de cette «sensibilité aux conditions initiales» ou S.C.I., véritable clef de la compréhension du chaos déterministe . Dans la pratique, le mot de chaos est donc devenu synonyme de chaos déterministe.

3. Où trouver la sensibilité aux conditions initiales?

La propriété de sensibilité aux conditions initiales (S.C.I.) avait déjà été pressentie vers 1875 par James Clerk Maxwell, puis par Henri Poincaré. Ensuite, le météorologiste, Edward Lorenz, étudiant les solutions d’un ensemble de trois équations différentielles ordinaires, qui représentaient un modèle très simplifié des écoulements dans l’atmosphère, remarqua que, en partant de conditions initiales légèrement différentes (et pour certaines valeurs des constantes, voir les équations ci-dessous), il obtenait des solutions tout à fait dissemblables au bout d’un même temps d’évolution (fig. 2). Et, pourtant, quoi de plus déterministe que ces équations:

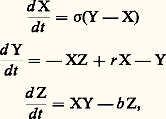dans lesquelles X, Y, Z représentent les trois variables du modèle et t le temps?

Les raisons de ce comportement, à première vue incompréhensible, ont été analysées et expliquées pour la première fois par David Ruelle et Floris Takens; en effet, ils ont montré en 1971 que la dépendance S.C.I., donc un comportement chaotique, pouvait apparaître dans un système dynamique ayant au minimum trois fréquences indépendantes (ce qui revenait à dire trois variables ou trois degrés de liberté), et dont les non-linéarités sont suffisantes.

De fait, le nombre minimal de degrés de liberté nécessaires pour que le chaos puisse apparaître peut être déduit de considérations topologiques se rapportant aux trajectoires dynamiques dans l’espace des phases (ou espace dont les coordonnées sont les variables dynamiques indépendantes du système). La trajectoire dans cet espace est le lieu des points correspondant aux valeurs prises par les variables à chaque instant. Ainsi l’espace des phases relatif au mouvement du pendule est un plan dont les coordonnées (variables) sont la position et la vitesse et dans lequel la trajectoire dynamique est une boucle fermée.

La propriété de S.C.I. se traduit par la divergence des trajectoires dans l’espace des phases. Or, dans un espace à deux dimensions, cette divergence entraînerait soit l’extension des trajectoires à l’infini, soit leur recoupement (ce qui ne peut avoir lieu, dans le premier cas, parce que les valeurs prises par les variables restent bornées et, dans le second cas, parce que la nature déterministe du phénomène interdit que les trajectoires se croisent). Il faut donc au minimum un espace de variables à trois dimensions pour que les trajectoires puissent diverger sans exploser à l’infini ou se couper. Assimilant le nombre de variables indépendantes à celui du nombre de degrés de liberté, on arrive à la conclusion qu’un système dynamique non linéaire ayant au minimum trois degrés de liberté peut devenir chaotique. L’exemple le plus simple est celui du pendule ou de l’oscillateur forcé par un «champ» périodique extérieur.

Imaginons, en effet, un pendule non linéaire entretenu en oscillation à sa fréquence propre f ¹; c’est un système à deux degrés de liberté: position et vitesse. S’il reste isolé, il ne peut devenir chaotique. Influençons son mouvement de manière périodique, par exemple en soumettant son axe à une oscillation de fréquence f ². Le système devient bipériodique (on dit aussi quasi périodique) mais, surtout, il a acquis un troisième degré de liberté: la phase de l’oscillation extérieure. C’est un fait que le système peut, maintenant, devenir chaotique et, en effet, pour certaines valeurs de l’amplitude du forçage extérieur, des mouvements désordonnés apparaissent.

4. Trois «scénarios vers le chaos»

Une des caractéristiques du chaos déterministe est de naître, puis de se développer continûment à partir d’un comportement ordonné, dont il ne perdra pas complètement mémoire. En partant du régime périodique, le chaos peut apparaître selon trois grandes catégories de processus couramment nommés «scénarios vers le chaos». Le régime périodique a souvent succédé lui-même à un régime stationnaire par augmentation de la contrainte appliquée au système, ou paramètre de contrôle; par l’augmentation de ce dernier, trois catégories d’événements peuvent se produire.

La première correspond au scénario via les intermittences. Celui-ci se caractérise par un régime qui demeure pratiquement périodique durant de longs laps de temps, et qui se déstabilise soudainement pour laisser place à une courte bouffée chaotique, puis le régime redevient périodique et ainsi de suite... La survenance des bouffées est elle-même irrégulière dans le temps, d’où une distribution des longueurs des phases périodiques (ou laminaires). Une autre caractéristique de ces intermittences est que, près du seuil de leur apparition, les bouffées sont rares et espacées alors que leur fréquence augmente quand on s’éloigne de ce seuil. Ce scénario, prévu théoriquement par Yves Pomeau et Paul Manneville en 1980, a été observé presque aussitôt après dans le cas de la convection de Rayleigh-Benard et dans une réaction chimique instationnaire.

Un autre scénario vers le chaos est le scénario par cascade de doublement de la période. Par augmentation progressive d’un paramètre de contrôle de l’expérience, le régime périodique voit tout d’abord sa période doubler puis être multipliée par 4, par 8, par 16, etc. Les seuils d’apparition de ces doublements successifs étant de plus en plus rapprochés, on atteint ainsi un point d’accumulation pour lequel il existe, en principe, une multiplication de la période de base jusqu’à l’infini. C’est là que le seuil du chaos est atteint. Habituellement attribué – pour ce qui est de sa découverte théorique – à Mitchell Feigenbaum (Los Alamos), ce modèle est l’aboutissement, en fait, de toute une série de travaux antérieurs, tant dans le domaine des mathématiques que dans celui de la physique. Indépendamment de Mitchell Feigenbaum, d’autres théoriciens aboutissaient, au même moment, à un résultat sensiblement identique, en particulier Pierre Coullet et Charles Tresser de la faculté des sciences de Nice. De nombreuses vérifications de l’existence et des propriétés de cette route ont été effectuées sur des systèmes très variés.

Le troisième type de scénario vers le chaos est également celui qui présente le plus de variantes. C’est le scénario de la quasipériodicité. Il se manifeste, d’une façon très qualitative, comme suit: par augmentation d’un paramètre de contrôle, le régime périodique devient quasi périodique, c’est-à-dire que son spectre contient deux fréquences de base indépendantes (incommensurables). Ce régime peut, à son tour, perdre sa stabilité et devenir chaotique soit directement, soit par la survenance d’une troisième fréquence. Dans cette dernière variante, la paternité en revient clairement à David Ruelle et Floris Takens. Comme dans les deux cas prédécents, divers exemples de ce modèle ont été trouvés expérimentalement dans bon nombre de systèmes.

Il est un système dynamique qui s’est révélé d’une grande richesse pour l’étude des scénarios menant au chaos, c’est l’instabilité hydrodynamique de Rayleigh-Benard. Considérons un fluide enfermé dans un récipient parallélépipédique dont les parois horizontales sont bonnes conductrices de la chaleur. Appliquons une différence de température T entre le bas et le haut de la couche, la partie basse étant à la température la plus élevée. Au-delà d’un certain seuil critique T^c , le liquide se met en mouvement avec ascension de fluide chaud et descente de fluide froid: c’est le phénomène de convection thermique. Point plus remarquable, une structuration périodique des mouvements du fluide apparaît sous la forme de rouleaux (ou tourbillons) convectifs. Ceux-ci ayant un diamètre de l’ordre de la hauteur de la couche, il suffit de travailler avec un récipient de dimension horizontale double de la hauteur pour n’avoir que deux rouleaux seulement, ce qui stabilise considérablement la structure vis-à-vis de complications d’origine spatiale. Par augmentation de la différence de température T (paramètre de contrôle), il peut alors se développer un, puis deux oscillateurs thermiques dans cette couche en convection. Le régime, stationnaire pour les valeurs modérées de T, devient donc périodique et éventuellement bipériodique pour les valeurs plus élevées du paramètre de contrôle. Étape ultime de l’évolution, il est possible, par une nouvelle augmentation de T, d’obtenir des régimes chaotiques.

5. Attracteurs étranges

Le chaos déterministe se rencontre aussi bien dans les systèmes hamiltoniens ou non dissipatifs (sans dissipation d’énergie vers l’extérieur) et dans les systèmes dissipatifs. Mais, dans ces derniers, la notion de chaos est intimement liée à celle d’attracteurs étranges.

En effet, la dynamique de tout système dissipatif non chaotique est telle que, à partir d’un ensemble de conditions initiales, elle converge vers un comportement unique d’équilibre, indépendant de ces conditions; cet état pourra être stationnaire dans le cas d’un pendule amorti, périodique pour un pendule entretenu, etc. La représentation de ces états dans l’espace des phases – point fixe, cycle limite, etc. – est un attracteur vers lequel convergent toutes les trajectoires situées dans le bassin d’attraction correspondant, de même que tous les ruissellements d’une même vallée aboutissent dans la rivière qui coule dans le fond.

Cette propriété de convergence, d’attraction vers la trajectoire d’équilibre est toujours présente quand le système devient chaotique, mais s’y rajoutent les effets dus à la S.C.I. Lorsque la trajectoire se construit au cours du temps dans l’espace des phases, il y a contraction suivant certaines directions et divergence suivant d’autres. Cette dernière se manifeste par des étirements, suivis de nécessaires repliements liés au fait que l’extension de l’attracteur est limitée par les valeurs extrémales prises dans le temps par les variables physiques. Résultat d’une multitude d’étirements et de repliements, l’attracteur chaotique est donc, en quelque sorte, fabriqué de la même manière que celle qu’utilise le boulanger pour faire sa pâte: il en résulte une structure feuilletée tout à fait caractéristique. Remarquons qu’entre les feuillets de l’attracteur chaotique il y a du vide que la trajectoire ne remplit jamais; bien qu’évoluant dans un espace à trois dimensions (dans le cas le plus simple) mais sans être confinée à une surface, la trajectoire ne remplit pas l’espace de façon dense. La dimension de l’attracteur, supérieure à 2, est donc inférieure à 3, de même que celle d’un arbre, objet pourtant non bidimensionnel, mais ne remplissant pas l’espace de façon dense. L’attracteur chaotique, de dimensionalité non entière, est donc un «fractal». Cet aspect est confirmé par le fait qu’on peut trouver des feuillets imbriqués à toutes les échelles d’observation, autre caractéristique curieuse des «fractals» (fig. 3). Ces propriétés topologiques ont fait nommer les attracteurs chaotiques «attracteurs étranges».

La présence de l’un de ces derniers dans l’espace des phases est une signature de chaos déterministe dissipatif. Aussi sa mise en évidence, à partir de signaux expérimentaux, est-elle cruciale. En effet, le nombre de degrés de liberté effectifs d’un système expérimental n’est généralement pas connu, et, dans ce cas, seule la démonstration de la présence des propriétés spécifiques du chaos déterministe sera valable, c’est-à-dire la démonstration de la présence ou non d’un attracteur étrange de faible dimensionalité dans l’espace des phases.

La manière la plus simple consiste à tracer l’attracteur lui-même à partir des variables du système. En fait, cette méthode se limite aux espaces des phases de faible dimensionalité (trois ou quatre au maximum); dans ce cas, et pour mieux cerner la topologie de l’attracteur, il est d’usage d’en faire une coupe par un plan (section de Poincaré, fig. 4). Cette démarche s’est révélée très fructueuse pour étudier la dynamique près du seuil d’apparition du chaos, en particulier pour suivre la déstabilisation des régimes périodiques l’ayant précédé. Mais, d’une part, cette manière de procéder n’amène pas d’élément quantitatif et, d’autre part, elle ne peut s’extrapoler à des systèmes complexes. Des moyens numériques ont donc été proposés pour tester la présence ou non d’un chaos déterministe.

Ils permettent, en particulier, de calculer la dimension fractale de l’attracteur qui donne une limite inférieure du nombre de degrés de liberté du système, permettant ainsi de démontrer la présence d’un comportement chaotique déterministe.

C’est ainsi qu’on a pu mettre en évidence des attracteurs étranges de basse dimensionalité (comprise entre un peu plus de 2 et 6) dans les domaines les plus variés, comme l’hydrodynamique, l’électronique, les systèmes électromécaniques, les semi-conducteurs, les lasers, certaines réactions chimiques, la biologie, certains équilibres écologiques comme les problèmes prédateurs-proie, etc.

La mise en évidence des phénomènes chaotiques a constitué une véritable révolution dans le monde de la pensée scientifique en ce sens qu’elle a, pour la première fois, fait éclater cette réalité que déterminisme et chaos (ou déterminisme et imprédictibilité) n’étaient plus opposés, idée qui, il n’y a pas si longtemps, aurait été pour le moins sacrilège.

Encyclopédie Universelle. 2012.